Zahřejte se pro mozek: můžete vyřešit problém s padělanými mincemi? Koukni na to!

Matematik má pouze tři pokusy, takže nemůžete vážit každou minci zvlášť. Musíte je rozdělit na hromádky a umístit je na váhy několik kusů najednou, postupně se přibližovat k falešnému.

Řekněme, že matematik se rozhodl rozdělit 12 mincí na tři hromádky po čtyřech mincích. Poté dal na každou stupnici čtyři mince. Toto vážení může přinést dva výsledky. Uvažujme o každém z nich.

1. Hmotnost dvou hromádek mincí byla stejná. Proto jsou všechny peníze v nich skutečné a padělky leží někde mezi čtyřmi neváženými mincemi.

Chcete-li sledovat výsledek, matematik označí všechny skripty nulou. Potom vezme tři z nich a porovná je se třemi neváženými mincemi. Pokud je jejich váha stejná, pak zbývající (čtvrtá) nevážená mince je padělaná. Pokud je váha odlišná, matematik přidá plus třem neoznačeným mincím, pokud jsou těžší než mince s nulami, nebo minus, pokud jsou lehčí.

Pak si vezme dva minceoznačené plus nebo minus a porovnává jejich hmotnost. Pokud je to stejné, pak zbývající kopie je falešná. Pokud ne, matematik se podívá na znamení: mezi mincemi s plusem bude falešný ten, který je těžší, mezi mincemi s mínusem, ten, který je světlejší.

2. Hmotnost dvou hromádek mincí nebyla stejná.

V tomto případě musí matematik jednat takto: označit peníze na těžké hromadě plusem, na lehké hromadě s mínusem, na nevážené hromadě s nulou, protože je známo, že falešná kopie byla na vahách.

Nyní musíte mince přeskupit, abyste udrželi zbývající dvě vážení. Jedním ze způsobů je vzít místo tří mincí s plusem, tři mince s minusem a na jejich místo umístit tři kusy s nulou.

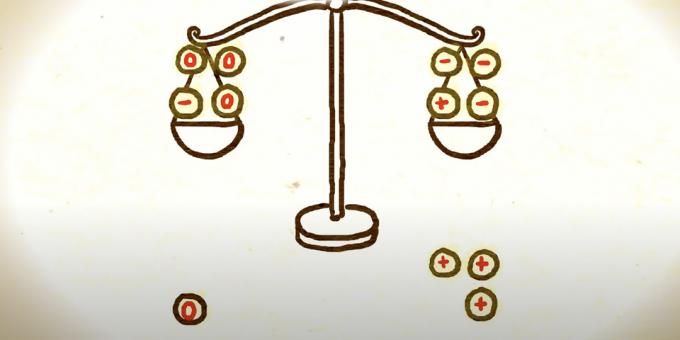
Následují tři možné možnosti. Pokud váha, která byla těžší, stále převáží, pak je buď stará mince se znaménkem plus těžší než ostatní, nebo mince se znaménkem minus na druhé straně stupnic. Matematik si musí vybrat kteroukoli z nich a porovnat ji s běžným vzorem, aby našel falešný.

Pokud se vážící deska, která byla těžší, stala lehčí, pak je jedna ze tří mincí se znaménkem mínus posunutých matematikem nejlehčí. Nyní musí porovnat dva z nich na vahách. Pokud jsou výsledky shodné, třetí mince bude padělaná. V případě nerovnosti je falešný jednodušší.

Pokud jsou misky po výměně vyvážené, je jedna ze tří mincí odstraněných z váhy se znaménkem plus těžší než ostatní. Matematik musí porovnat dva z nich. Pokud jsou si rovni, třetí je falešný. V případě nerovnosti je falešný ten, který je těžší.

Císař souhlasně přikývl, když poslouchal úvahy matematika, ale nepoctivý guvernér jde do vězení.

Tato hádanka je překladem videa TED-Ed.